As Equações Exponenciais, são aquelas expressões cuja incógnita aparece somente, ou na maioria das vezes, em seu expoente. Existem maneiras diferentes de resolver estas equações, sendo que uma delas é:
Igualdade de potências de mesma base.
Assim, obtemos a seguinte expressão:
A expressão acima representa uma igualdade entre as potencias. Assim a mesma base, sendo que também possuem expoentes desiguais, as respectivas incógnitas: . Para formar uma igualdade entre as bases podemos trabalhar apenas com os números expoentes e assim, cancelar as bases, igualar ambos e formar o .
É de estrema importância que você entenda que a base de nossas potencias não devem ser números avulsos. Mas sim, sempre números maiores que zero e diferente do valor 1. As definições de expoentes nos deixam bem cientes destas funções.
Basicamente, para resolver as equações exponenciais, você deve encontrar o valor das incógnitas que nelas aparecem. Para que isso ocorra, é necessário que você entenda as seguintes funções:
- Propriedades de potência;
- Equação de primeiro grau.
Ambos conhecimentos prévios, o ajudarão muito a resolver as equações exponenciais. Por isso, antes mesmo que tende resolve-las, dê uma breve olhada nesses conteúdos.
Sabendo que os números são maiores que zero e diferentes de 1, você deve saber que as potencias de bases iguais seguem o seguinte cálculo:
Veja a seguir, um exemplo:
Uma vez que você percebe que o valor 27 é exatamente igual ao valor 33. Podemos substituir esses mesmos valores na equação e assim, teremos:
De fato, você pode notar que as bases também são iguais. Então, podemos agora, utilizar a propriedade, mencionada acima, das equações exponenciais. Assim, obtemos o seguinte resultado:
Resolvendo exercícios
Exercício n° 1 –
Sabendo das propriedades citadas acima, determine a solução da seguinte equação exponencial.
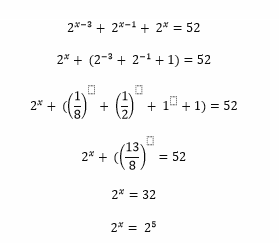
Exercício n° 2 –
Sabendo das propriedades citadas acima, determine a solução da seguinte equação exponencial e determine o valor de x na expressão.
Descubra então que 
Onde 
Levando a solução de (1,2)